 Value at Risk ou simplesmente valor em risco ou, ainda, valor que se pode perder.
Value at Risk ou simplesmente valor em risco ou, ainda, valor que se pode perder.
VaR teve sua origem na gestão de ativos e passivos (ALM – asset liability management), com o objetivo de medir o risco dos descasamentos de prazos de fluxos a pagar e fluxos a receber em função das oscilações de preços do mercado dos instrumentos financeiros envolvidos.
Quando adicionado às estratégias de uso de diversos fatores de risco para cobertura cruzada de ativos e passivos, o VaR se mostrou tão promissor que foi rapidamente absorvido na cultura de gestão de risco em investimentos.
Mas o que é VaR?
VaR é uma forma simples de se medir o valor da perda máxima de um investimento. Analisando apenas um ativo e observando a oscilação histórica de preços deste ativo, pode-se dizer que o valor em risco é igual ao tamanho histórico destas oscilações. Por exemplo, se um ativo costuma subir e descer aproximadamente 10% de seu preço, podemos dizer que existe um risco médio de se perder no máximo 10% do investimento no ativo independente do dia da aplicação. Isto é VaR.
VaR é só isso?
Sim e não.
Sim, porque é realmente uma medida de perda baseada nas oscilações históricas.
Não, porque tem alguns poucos detalhes a mais. Poucos, mas relevantes.
O importante de cada um destes detalhes adicionais é entender o quanto eles fragilizam o resultado e o primeiro detalhe em discussão é a confiança do VaR.
Confiança do VaR
VaR é um modelo matemático de previsão de perdas. Por sua natureza como modelo, pode funcionar ou falhar.
Falhar não significa que a perda foi superior ao previsto, mas que a perda foi superior ao previsto mais vezes do que se esperava. Estabelecer a confiança é estabelecer esta definição de falha do modelo.
Confiança do VaR pode ser, portanto, entendida como a quantidade de vezes que o modelo não ultrapassará a perda máxima. Como o 100% é inatingível, tem-se que escolher um número menor e real.
Para auxiliar esta escolha, utiliza-se o modelo estatístico da curva de distribuição normal. É o modelo mais comum de distribuição, sendo definido apenas por média e variância. O único problema é que os ativos financeiros e seus retorno (ou oscilações de preços) não respeitam este tipo de comportamento. Eles têm uma distribuição aproximadamente log-normal: caem no máximo 100% e podem subir ilimitadamente (atenção ao destaque da palavra aproximadamente).
Por outro lado, esta distribuição log-normal tem a característica de seu logaritmo ter uma distribuição normal. Ou seja, aplicando o logaritmo dos retornos, modifica-se os preços históricos dos ativos para uma distribuição normal. Isto é bom.
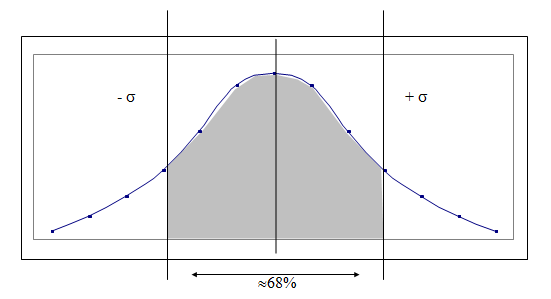
De posse da distribuição normal, pode-se estabelecer a confiança pela escolha do multiplicador do desvio-padrão, lembrando que dentro de 1 desvio-padrão para cada lado da média tem-se cerca de 68% das possibilidades. Utilizando 1,65 desvios-padrão (bicaudal – perda ou ganho), tem-se cerca de 90% das possibilidades cobertas ou 95% das perdas cobertas.
Não é incomum encontrar em algumas instituições definições de confiança de VaR acima de 95%. Muitas vezes, 99%. Este patamar de confiança é mais conservador do que 95%, pois será utilizado um multiplicador maior para o desvio-padrão. Isto porém, pode ser a primeira armadilha.
A confiança não define a eficiência do modelo. Define o que significa a falha do modelo. Uma confiança de 99% do modelo equivale a dizer que ele só pode falhar 1% das vezes. Para isto ser verdade, o “aproximadamente log-normal” já não pode ser tão aproximadamente assim.
Em resumo, uma confiança de VaR alta exige muita performance do modelo e muita estabilidade (de comportamento) das séries financeiras envolvidas, o que costuma gerar uma falsa sensação de conservadorismo do valor em risco.
Ainda falta discutir outros detalhes, mas por agora, 95% de confiança parece bastante suficiente.
Qual a sua?
O modelo de VaR, suas variações e parâmetros são ferramentas do Sistema de Risco de Mercado, integrante da Plataforma Integrada de Risco Duxus (http://www.duxus.com.br).
